Finding the area of an amorphous figure in MATLAB

Imagine that you have two series of data (nx1). Imagine that these data come from two sensors measuring the displacement of a particle around a certain point, something like this:
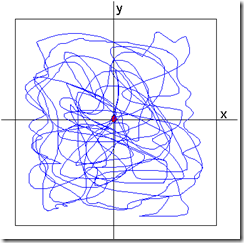
  The sensors measure the position X-Y 100 times each second and you measure for 30 seconds. At the end you will have two vectors containing 3000 samples each one.
Something like this:
x=[3,6,7,5,3,2,3,7,8,9,7,5,3,2,12,3,5,7,8……...n]
y=[2,4,5,6,7,3,5,3,2,5,7,43,6,8,4,2,4,6,7,……..n]
From these vectors of data you must to calculate the area  drawn by the (x,y) values, the contour of the image.



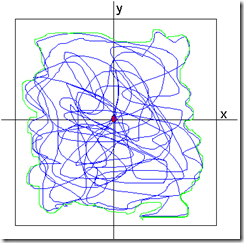
Here I present a numeric method to do that using the X  and Y values. Albeit, the calculated area is only an approximation, sometimes, that is enough.
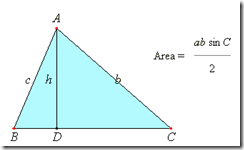
The method is based on trigonometry. Basically, the shape will be divided into sections of one degree as showed on the figure 3. The maximum value between each portion of the figure will be used to calculate the area by adding the area of each portion.

Suppose that, between 0 and 1 degree, the maximum value of r
r=sqrt(x^2+y^2)
is 0.5. The maximum value between 1 and 2 degrees is 0.7, and so on. We calculate all those maximums and at the end we will have a set of magnitude separated by approximately one degree. Now is only necessary to calculate de area between two of these consecutive magnitudes and add the value of each portion of area to the others sub parts.

This will result in an approximation of the whole area of the figure. Obviously, there are several errors because the separation between each point is not one degree necessarily, and the contour is not square. Anyway, the approximation probes to be useful for some cases.
Of course, there are many other methods, this is just one of these and no necessarily is the best, is just an attempt. Now, below is the implementation using MATLAB.

Real graph in MATLAB from two vectors of 3000x1 data.  The blue line joins all the 3000 points of data. The red line joins the maximum vectors using angles of 8 degrees.  Area=134.06

Same that the figure to the right but  using angles of 3 degrees. Area = 110.73 The area is less because the algorithm finds the vectors with more precision making the envelope tighter.

%Script to calculate the area of an eneveloped made by to vectors X, Y.
%plotted X vs Y Both vectors have the same length.
%Input: X and Y vectors, deg (resolution of the envelope. integer max value
%90, a value around 8 is optimus, check graphic resultant).
%Output: Area of the envelope
function out=area_x_y(x,y,deg)
plot (x,y);
vd=360/deg;
for i=1:length (x)
r(i,1)=sqrt(x(i,1)^2+y(i,1)^2);       %calcula la magnitud del vector formado por x y y
if (x(i,1)>0&y(i,1)>0)                %Grados para el primer cuadrante   x+ y+
teta(i,1)=atan(y(i,1)/x(i,1))*180/pi;
end
if (x(i,1)<0&y(i,1)>0)                %Grados para el segundo cuadrante   x- y+
teta(i,1)=(atan((y(i,1)/x(i,1)))*180/pi)+180;
end
if (x(i,1)<0&y(i,1)<0)                %Grados para el tercer cuadrante   x- y-
teta(i,1)=(atan((y(i,1)/x(i,1)))*180/pi)+180;
end
if (x(i,1)>0&y(i,1)<0)                %Grados para el cuarto cuadrante   x+ y-
teta(i,1)=(atan((y(i,1)/x(i,1)))*180/pi)+360;
end
end
vectores=zeros(vd,2);           %Made matrix to save r and teta (polar)
xy=zeros(vd,2);                 %matrix to save maximum x and y of r and teta (cartesian)
for ang=0:deg:360-deg
max_ang=zeros(3001,1);
for i=1:length(teta)
if ((teta(i,1)>=ang)&(teta(i,1)<(ang+deg))) 
rmax(i,1)=r(i,1);
else
rmax(i,1)=0;
end
end
[maxr(ang+1,1) indice]=max(rmax);       %maximum vector between the angle determined
vectores(ang/deg+1,:)=[r(indice,1) teta(indice,1)]; 
xy(ang/deg+1,:)=[x(indice,1) y(indice,1)];
%    plot (x(indice,1), y(indice,1));
%    hold on
end
r=vectores(:,1);
teta=vectores(:,2);
%Calculating the area of each trangle
for i=1:1:length (teta)-1
dif_angle(i,1)=teta(i+1,1)-teta(i,1);       %Delta of angle
sub_area(i,1)= r(i,1)*r(i+1,1)*(sin(dif_angle(i,1)*pi/180))/2; %(r1*r2*sin(Theta))/2
end
%calculate the last segment which is not considered in the loop above
a1=(360-teta(end,1))*pi/180;        %Last angle value *rads
a2=teta(1,1)*pi/180;                %First angle value *rads
dang=a1+a2;                 %angle between the last and the first vector
sub_area2=r(1,1)*r(end,1)*sin(dang)/2;      %Last portion of the area
area=sum(sub_area)+sub_area2;
out=area;
clear a1 a2 dang sub_area2 sub_area i ang maxr max_ang rmax vd vectores diff_angle indice teta r
plot (xy(:,1),xy(:,2),'red','LineWidth',2);
hold on
plot (x,y);
hold off

UPDATE:
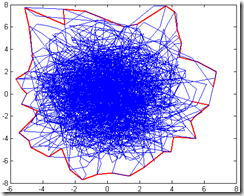
The script in matlab use the real angle between magnitudes, then the results is more accurate. It is recommendable to check the graph given by the script in order to decide which value of deg is best suitable for your requirements.
A value of 8 degrees (deg=8) which means that the 360 degrees are divided in 72 parts to calculate the envelope was more appropriate for me looking at the graph.